Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.Example 3:
Input: root = [1,2], p = 1, q = 2
Output: 1Constraints:
- The number of nodes in the tree is in the range
[2, 105]. -109 <= Node.val <= 109- All
Node.valare unique. p != qpandqwill exist in the tree.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// Now you have a binary tree and root is the root of the tree.
// p and q are the two nodes in this tree.
// p and q have the common descendant. They have many descendants. But i need to find the lowest one.
// I should keep finding their parent util their parent in the same level.
// Every time their parents are int the same level, check if they are the same node.
// traverse the whole tree and make a parent map={{node: parent}} and depth[node]=depth.
// depth of root node is 1, pop and push two new nodes in stack and their depth are previous poped node depth+1
if(root==NULL){
return root;
}
stack<TreeNode*> s;
s.push(root);
map<int,int> depth;
map<TreeNode*,TreeNode*> parent;
set<int> visited;
//init parent, every node's parent is itself.
parent[root]=root;
depth[root->val]=1;
while(!s.empty()){
TreeNode* curr=s.top(); s.pop();
visited.insert(curr->val);
int d=depth[curr->val];
if(curr->right!=NULL){
s.push(curr->right);
depth[curr->right->val]=d+1;
parent[curr->right]=curr;
}
if(curr->left!=NULL){
s.push(curr->left);
depth[curr->left->val]=d+1;
parent[curr->left]=curr;
}
//if both p and q are visited, then break in advance
if(visited.count(p->val) && visited.count(q->val)) {
break;
}
}
TreeNode* pParent=p, *qParent=q;
//every node has its parent except for the root
while(parent[pParent]->val!=pParent->val || parent[qParent]->val!=pParent->val){
if(depth[pParent->val]==depth[qParent->val]) {
if(pParent->val==qParent->val) {
return pParent;
}else{
pParent=parent[pParent];
qParent=parent[qParent];
}
}
//if pParent depth < qParent depth, then qParent should be higher
else if(depth[pParent->val]<depth[qParent->val]){
qParent=parent[qParent];
} else {
pParent=parent[pParent];
}
}
return root;
}
};Use recursion can be more efficient because using map in each loop.
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//discuss conditions from leaf to root
// if curr is child of leaf, then return null
// if curr is a leaf:
// if curr finds p or q, then return curr
// if curr is parent of left and right:
// if curr finds p or q, then return curr
// else:
// if curr.left finds one and curr.right also finds one, then return curr.
// if curr.left finds one and curr.right does not find, then another one may be child of that one or does not exist in curr tree. No matter which condition, return current tree.
// if right.left finds one and curr.left does not find, the same as above.
// if no one found, then return NULL;
if(!root){
return NULL;
}
if(root->val==p->val || root->val==q->val){
return root;
} else {
TreeNode* left=lowestCommonAncestor(root->left, p, q);
TreeNode* right=lowestCommonAncestor(root->right, p, q);
if(left&&!right){
return left;
}else if(!left&&right){
return right;
}else if (left&&right){
return root;
} else {
return NULL;
}
}
}
};Note:
All return value will point to left and right because left and right is the entrance.
This method is also easy to understand.
We store the path of root to n1 and root to n2. if path1=[root, n1] and path2=[root, n2], then first mismatch is n1!=n2. The previous node is their LCA.
class Solution {
public:
bool findPath(TreeNode* root, vector<TreeNode*> &path, int target) {
//if curr is child of leaf, then return null
//if curr is root:
//insert current val
//check if current val equals target then return true
//else:
//if left child finds, then return true
//if right finds, then return true
//if not found, then target does not exist in curr tree, then we should go back and clear our footprint
if(!root) return root;
path.push_back(root);
if(root->val==target){
return true;
}
bool left=findPath(root->left, path, target);
bool right=findPath(root->right, path, target);
if(left || right){
return true;
}else{
path.pop_back();
return false;
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
vector<TreeNode*>path1;
vector<TreeNode*>path2;
// p and q all exist in the tree, so we don't need to check
findPath(root,path1,p->val);
findPath(root,path2,q->val);
int i;
for(i=0; i<path1.size() && i<path2.size();i++){
//if equal, then continue, else break
if(path1[i]->val!=path2[i]->val) {
break;
}
}
return path1[i-1];
}
};Tarjan's off -line LCA is not efficient in this problem, but i just want to practice.
You can find more details on https://www.geeksforgeeks.org/tarjans-off-line-lowest-common-ancestors-algorithm/.
class Solution {
unordered_map<TreeNode*, TreeNode*> parent;
unordered_map<TreeNode*, TreeNode*> child;
unordered_map<TreeNode*, TreeNode*> sibling;
unordered_map<TreeNode*, bool> visited;
TreeNode* pp, *qq;
TreeNode* ans;
public:
//init parent, child, sibling
void LCA(TreeNode* root){
if(!root) return;
// init parent
parent[root]=root;
//if left and right are not null
if(root->left){
child[root]=root->left;
}
if(!root->left&&root->right){
child[root]=root->right;
}
if(root->left&&root->right){
sibling[root->left]=root->right;
}
LCA(root->left);
LCA(root->right);
}
// x be the parent
void unionSet(TreeNode* x, TreeNode* y) {
//find root of x
TreeNode* xroot=findSet(x);
//find root of y
TreeNode* yroot=findSet(y);
parent[yroot]=xroot;
}
TreeNode* findSet(TreeNode* x) {
//keep find the parent util itself
while(parent[x]!=x){
x=parent[x];
}
return x;
}
void walk(TreeNode* root) {
if(!root) return;
//go to leftest and set its parent and ancestor
TreeNode* node=child[root];
while(node) {
//walk left
walk(node);
//union root and node
unionSet(root,node);
//walk right
node=sibling[node];
}
// if curr equals one of targets, then set visited
// if another target B has been visited, then B's ancestor is the LCA
// ans=findSet(B);
// if another target A has been visited, then A's ancestor is the LCA
// ans=findSet(A)
if(ans) {
return;
}
if(root->val==pp->val || root->val==qq->val) {
visited[root]=true;
if(root->val==pp->val && visited[qq]){
// find another qq
ans=findSet(qq);
return;
}
if(root->val==qq->val && visited[pp]){
ans=findSet(pp);
return;
}
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//subset[root].child=root->left
//init subset
LCA(root);
pp=p; qq=q;
walk(root);
return ans;
}
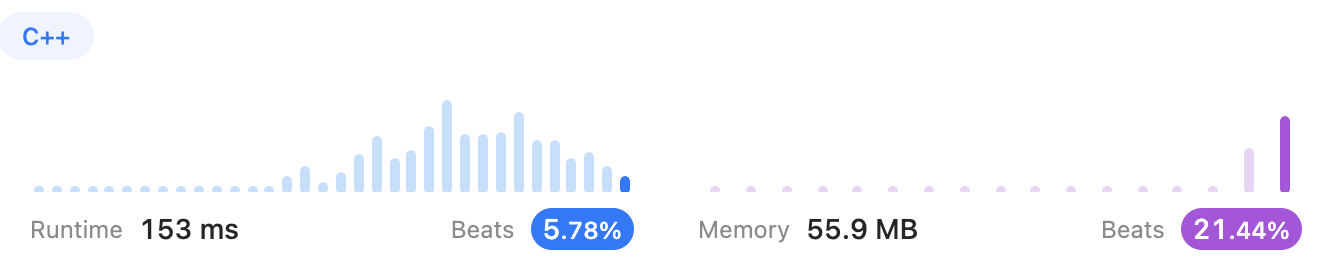
};And then we can use path compression to make it quicker. But i don't know why leetcode tells me the program gets slower and use more memory.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
unordered_map<TreeNode*, TreeNode*> parent;
unordered_map<TreeNode*, TreeNode*> child;
unordered_map<TreeNode*, TreeNode*> sibling;
unordered_map<TreeNode*, bool> visited;
TreeNode* pp, *qq;
TreeNode* ans;
public:
//init parent, child, sibling
void LCA(TreeNode* root){
if(!root) return;
// init parent
parent[root]=root;
//if left and right are not null
if(root->left){
child[root]=root->left;
}
if(!root->left&&root->right){
child[root]=root->right;
}
if(root->left&&root->right){
sibling[root->left]=root->right;
}
LCA(root->left);
LCA(root->right);
}
// x be the parent
void unionSet(TreeNode* x, TreeNode* y) {
//find root of x
TreeNode* xroot=findSet(x);
//find root of y
TreeNode* yroot=findSet(y);
parent[yroot]=xroot;
}
TreeNode* findSet(TreeNode* x) {
//keep find the parent util itself
while(parent[x]!=x){
x=parent[x];
}
return x;
}
void walk(TreeNode* root) {
if(!root) return;
//go to leftest and set its parent and ancestor
TreeNode* node=child[root];
while(node) {
//walk left
walk(node);
//union root and node
unionSet(root,node);
//walk right
node=sibling[node];
}
// if curr equals one of targets, then set visited
// if another target B has been visited, then B's ancestor is the LCA
// ans=findSet(B);
// if another target A has been visited, then A's ancestor is the LCA
// ans=findSet(A)
if(ans) {
return;
}
if(root->val==pp->val || root->val==qq->val) {
visited[root]=true;
if(root->val==pp->val && visited[qq]){
// find another qq
ans=findSet(qq);
return;
}
if(root->val==qq->val && visited[pp]){
ans=findSet(pp);
return;
}
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//subset[root].child=root->left
//init subset
LCA(root);
pp=p; qq=q;
walk(root);
return ans;
}
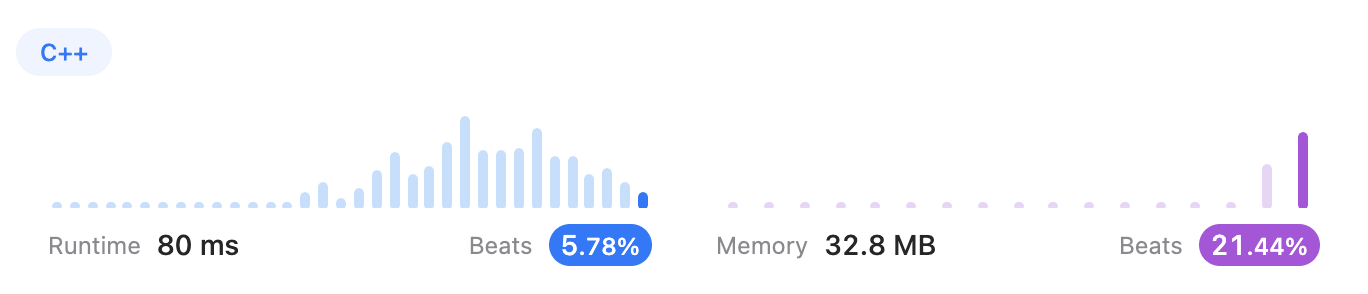
};I think it is because i use multiple map, i should merge them into a subset. I think it works as image shows.
typedef struct {
TreeNode* ancestor;
TreeNode* parent;
TreeNode* child;
TreeNode* sibling;
bool visited;
int rank;
} subset;
class Solution {
unordered_map<TreeNode*, subset> subset;
TreeNode* pp, *qq;
TreeNode* ans;
public:
//init parent, child, sibling
void LCA(TreeNode* root){
if(!root) return;
// init parent
subset[root].ancestor=root;
subset[root].parent=root;
subset[root].ancestor=root;
subset[root].rank=0;
//if left and right are not null
if(root->left){
subset[root].child=root->left;
}
if(!root->left&&root->right){
subset[root].child=root->right;
}
if(root->left&&root->right){
subset[root->left].sibling=root->right;
}
LCA(root->left);
LCA(root->right);
}
// x be the parent
void unionSet(TreeNode* x, TreeNode* y) {
//find root of x
TreeNode* xroot=findSet(x);
//find root of y
TreeNode* yroot=findSet(y);
//if rank equal then x be parent
if(subset[xroot].rank==subset[yroot].rank){
subset[yroot].parent=xroot;
subset[xroot].rank++;
}else if(subset[xroot].rank<subset[yroot].rank){
subset[xroot].parent=yroot;
}else{
subset[yroot].parent=xroot;
}
//else if node with higher rank be the parent
}
TreeNode* findSet(TreeNode* x) {
//keep find the parent util itself
while(subset[x].parent!=x){
x=subset[x].parent;
}
return x;
}
void walk(TreeNode* root) {
if(!root) return;
//go to leftest and set its parent and ancestor
TreeNode* node=subset[root].child;
while(node) {
//walk left
walk(node);
//union root and node
unionSet(root,node);
//walk right
subset[findSet(node)].ancestor=root;
node=subset[node].sibling;
}
// if curr equals one of targets, then set visited
// if another target B has been visited, then B's ancestor is the LCA
// ans=findSet(B);
// if another target A has been visited, then A's ancestor is the LCA
// ans=findSet(A)
if(ans) {
return;
}
if(root->val==pp->val || root->val==qq->val) {
subset[root].visited=true;
if(root->val==pp->val && subset[qq].visited){
// find another qq
ans=subset[findSet(qq)].ancestor;
return;
}
if(root->val==qq->val && subset[pp].visited){
ans=subset[findSet(pp)].ancestor;
return;
}
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//subset[root].child=root->left
//init subset
LCA(root);
pp=p; qq=q;
walk(root);
return ans;
}
};We can also use mutation of tarjan's LCA. The core is the visited mark.
typedef struct {
TreeNode* ancestor;
TreeNode* parent;
bool visited;
int rank;
} subset;
class Solution {
unordered_map<TreeNode*, subset> subset;
TreeNode* pp, *qq;
TreeNode* ans;
public:
// x be the parent
void unionSet(TreeNode* x, TreeNode* y) {
//find root of x
TreeNode* xroot=findSet(x);
//find root of y
TreeNode* yroot=findSet(y);
//if rank equal then x be parent
if(subset[xroot].rank==subset[yroot].rank){
subset[yroot].parent=xroot;
subset[xroot].rank++;
}else if(subset[xroot].rank<subset[yroot].rank){
subset[xroot].parent=yroot;
}else{
subset[yroot].parent=xroot;
}
//else if node with higher rank be the parent
}
TreeNode* findSet(TreeNode* x) {
//keep find the parent util itself
while(subset[x].parent!=x){
x=subset[x].parent;
}
return x;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//init subset[root]
//go to left child
//union current and left
//go to right child
//union current and right
TreeNode* res=NULL;
if(!root) return NULL;
subset[root].parent=root;
subset[root].ancestor=root;
if(root->left) {
res=lowestCommonAncestor(root->left, p, q);
unionSet(root, root->left);
subset[findSet(root->left)].ancestor=root;
if(res){
return res;
}
}
if(root->right){
res=lowestCommonAncestor(root->right, p, q);
unionSet(root, root->right);
subset[findSet(root->right)].ancestor=root;
if(res){
return res;
}
}
//if curr find any of targets
//if curr finds target A and B is visted, then B's ancestor is LCA
//if curr finds target B and A is visited, then A's ancestor is LCA
if(root->val==p->val || root->val==q->val) {
subset[root].visited=true;
if(root->val==p->val && subset[root].visited) {
return subset[findSet(q)].ancestor;
}
if(root->val==q->val && subset[root].visited) {
return subset[findSet(p)].ancestor;
}
}
return res;
}
};